DYNAMIC MECHANICAL ANALYSIS (DMA)

Dynamic mechanical analysis (DMA) is a thermal analysis technique used to measure changes in the viscoelastic response of a material as a function of temperature, time, or deformation frequency by subjecting it to a small,(usually sinusoidal) oscillating force.

1. Dynamic mechanical analysis characterizes the viscoelastic properties of materials.
2. Solid materials store applied energy and use it to recover from the deformation induced by the applied 3. Liquids dissipate applied energy as heat and hence are unable to recover their structure.
4. Many polymeric materials exhibit both elastic (solid) and viscous (liquid) properties and hence are viscoelastic.. Dynamic mechanical analysis is best for that.
5. Viscoelastic will exhibit phase angles (delta) between 0-90°. The phase angle is used to determine the parameters like storage modulus, loss modulus, tan (delta) etc.

Terminology
Storage Modulus (E’): It is defined as the energy stored during a loading cycle and represents the stiffness of a viscoelastic material. It is also roughly equal to the elastic modulus and is expressed in MPa.
Loss Modulus (E”): It is defined as the energy dissipated during one loading cycle. It represents energy lost as heat and is a measure of vibrational energy that has been converted during vibration and that cannot be recovered. It is expressed in MPa.
Complex Modulus (E*): It is defined as the ratio of the stress amplitude to the strain amplitude. It represents the stiffness of the material.
Phase Angle delta: It is the phase difference between the dynamic stress and the dynamic strain in a viscoelastic material subjected to sinusoidal oscillation. It is expressed in radian.
Loss Factor (tan delta): It is the ratio of loss modulus to storage modulus. It is a measure of the energy lost in terms of recoverable energy and represents the mechanical damping or internal friction in a viscoelastic system. A low tan delta value is indicates that the material is more elastic. It is dimensionless.

Test method: ASTM D4092, ISO 6721-1
Significance
1. It is most useful for observing the viscoelastic nature of polymers. DMA is commonly used to determine quantitative flexural storage and loss moduli, shear storage and loss moduli, tan, and the dynamic and complex viscosity of materials.
2. DMA is useful for qualitatively characterizing the glass transition temperature and other sub-Tg transitions of polymer and composite materials. Transition temperatures are readily obtained by determining the peak temperatures of the loss moduli or tan delta profiles.
3. DMA is an invaluable tool for researchers to assess the temperature and time dependent behavior of materials under load.

Three-point bending:
1. The ends of the sample are freely supported and the load is applied to the midpoint.
2.To ensure direct contact with the specimen, an additional inertial member needs to be applied.
3. This test arrangement is suitable for very stiff materials, such as metals, ceramics, and composites.
4. It is unsuitable for amorphous polymers because they soften extensively above the Tg.
5. It is a simple arrangement, but additional shear stress in the midpoint plane of the specimen must be taken into account.

6. With short specimens, this gives rise to interlaminar shear stress in the neutral, usually shear-soft plane.
7. The effect can be reduced by employing either an appropriate length/thickness ratio or a four-point arrangement, which is usually more complicated.

Dual cantilever bending:
1. The specimen is clamped to both supports and, at its midpoint, to the push-rod stress.
2. Consequently, no inertial member is needed.
3. This test arrangement is used for reinforced thermosets, thermoplastics, and elastomers.
Single cantilever:
1. Specimens that expand considerably when heated may distort in a dual cantilever arrangement, and this can falsify the readings.
2. For such specimens, a single cantilever or freely supported arrangement is best.
3. While a specimen experiences alternate compression and tension mainly along its length in flexural loading, it experiences homogeneous stress down its longitudinal axis when either tension or compression is applied exclusively.
Tensile mode
1. Clamped at top and bottom, the specimen is subjected to an underlying tensile stress to prevent it from buckling during dynamic loading.
2. Tensile mode is ideal for examining thin specimens, such as films and fibers in the low-to medium modulus range.
Compression Mode
1. In compression mode an axial load is applied to mostly specimens held between
two parallel plates.
2. Soft rubbers on gelations pastes are most suitable for this measurement.
3. Uniaxial compression effects a one-dimensional change in the specimen’s
geometry whereas bulk compression effects a three-dimensional change.
4. Uniaxial compression can cause thin specimens to buckle.
5. On short, thick specimens, hindered deformation at the supports makes it difficult to make accurate determination of the modulus.
Shear Loading
1. It consists of a sandwich arrangement in which two specimens are subjected to cyclical shear by the displacement of a central push-rod.
2. Like compression loading, axial shear loading is suitable for soft materials.
Advantage
3. DMA techniques are very sensitive to temperature changes.
4. Secondary transitions observed by DSC or DTA techniques are clearly evidenced by DMA.
5. Any thermal transition in polymers will generate a peak for tand and E”
6. The peak maxima for E” and tand do not occur at the same temperature.

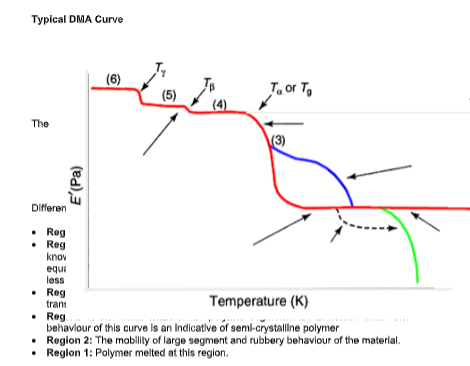
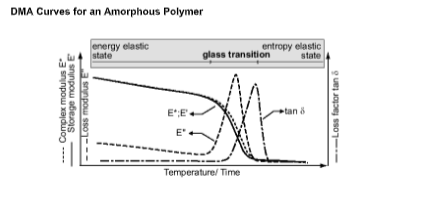
The material is said to be in the glass state or energy elastic state at the low temperatures and in the rubber or entropy elastic state at the elevated temperatures mentioned in the above figure. A change from the glass state into the rubber-elastic state is called the glass transition. When the timescale of molecular motion coincides with that of mechanical deformation, each oscillation is converted into the maximum- possible internal friction and non-elastic deformation. The loss modulus, which is a
measure of this dissipated energy, reaches a maximum. In the glass transition region, the storage modulus falls during heating to a level of one-thousandth to one ten-thousandth of its original value. As the loss factor is the ratio of the loss modulus to the storage modulus, the drop in storage modulus suppresses the increase in the loss factor initially; the temperature at which the loss factor is a maximum is therefore higher than the temperature corresponding to maximum loss modulus.

Applications
1. Analysis of resin and adhesive cure
2. Determination of the degree of crosslinking in plastics
3. Analysis of polymers
4. Analysis of a wide variety of materials used in healthcare, food, and other application.
5. Glass transitions (primary, secondary, etc.) m which is more sensitive than DSC!
6. Quantification of gelation (ex: sol-gel transition).
7. Polymer morphology/compatibility
8. Interaction between polymeric components or between drug molecules and polymeric constituents of pharmaceutical/biomedical systems.